這道題目第一個測資比較簡單,但第二個測資我很堅持求公式解但還是失敗了,但至少有得到角度,還好最後發現官方提供一些訊息(比賽結束的解析),但發現其實題目就有說算凸包了,雖然還有更快的作法但沒有去實作它,最後也多學到了一個新的演算法。
原題目
一駕神秘的太空船出現在這個天空中,天空是三維空間的平面,在y = -3 km與xz平面平行。外星人的船是一個邊長1公里的實心立方體,中心(0km,0km,0km),八個角(+/- 0.5km,+ / - 0.5km,+ / - 0.5km) 。這艘船投影了一個影子,陰影是立方體在平面上的正交投影。(太陽是沿著y軸在天空上方無限遠的點。)
只要外星人滿足軍方的要求,軍方就願意容忍這艘船:陰影面積覆蓋只可接近Akm^2。我們了解船隻不能改變尺寸,傳的中心不能移動但是傳可以任意旋轉到位。
請找到一個方式,使陰影面積最接近外星人可旋轉角度。使用三個點表達你的旋轉。
只要外星人滿足他們的官僚要求,軍方就願意容忍這艘船:陰影必須覆蓋可接受地接近A km 2的飛機區域(參見輸出部分以獲得精確的定義)。他們聘請了一位幾何語言學專家來向外國人傳達這種需求。在你的通訊中,到目前為止,你已經了解到船隻不能改變尺寸,船的中心不能移動,但船隻能夠任意旋轉到位。
請找到一種方式,使陰影的面積接近外星人可以旋轉角度。(x.y.z的座標)。
輸入第一行T為測試筆數,A為所需陰影面積km^2單位,小數點六位。
至少會有一種方法可以旋轉太空船。
每個測試,首先輸出一行Case #x:,x是測試編號(從1開始)。然後,輸出另外三行,如上所述,三個提供的面中心之一的x,y和z坐標。可使用小數(例如,0.000123456)或科學記號(例如,1.23456e-4)。
當且僅當滿足以下所有條件時,您的答案才是是正確的:
1.從每個點到原點的距離(以km為單位)必須介於0.5 - 10^-6和0.5 + 10^6之間。
2.連接原點到每個點的段之間的角度(以弧度表示)必須在π / 2 - 10^6和π / 2 + 10^-6之間。
3.陰影區域(以km^2為單位),通過將所有8個頂點投影到y = -3平面上並找到那些投影點的凸包區域計算得出,必須介於A - 10^-6和 A + 10^-6之間。(後面不太瞭解意思大概是說它答案檢測是用向量加法之類)
請注意,您可能需在小數點後輸出超過6位數才能通過。如果有多個可接受的答案,您可以輸出其中任何一個。
1 ≤ T ≤ 100.
時間限制: 30秒.
記憶體限制: 1GB.
測試1
1.000000 ≤ A ≤ 1.414213
測試2
1.000000 ≤ A ≤ 1.732050
2
1.000000
1.414213
Case #1:
0.5 0 0
0 0.5 0
0 0 0.5
Case #2:
0.3535533905932738 0.3535533905932738 0
-0.3535533905932738 0.3535533905932738 0
0 0 0.5
這題主要就是要我們求它x.y.z旋轉矩陣,圖片來源3D小畫家。
三角函數:
cos(角度(弧度)) = 鄰邊 / 對邊
角度弧度 = acos(鄰邊 / 對邊)
旋轉矩陣:
這部分因為題目是投影到xz平面因此我的想法是把z和y旋轉矩陣做交換(應該可以用原本的不用這樣做)。
依序上到下左到右都是x.y.z位置。
繞著x軸 = [1, 0, 0]
[0, cos(度), sin(度)]
[0, -sin(度), cos(度)]
繞著y軸 = [cos(度), 0, -sin(度)]
[0, 1, 0]
[sin(度), 0, cos(度)]
繞著z軸 = [cos(度), sin(度), 0]
[-sin(度), cos(度), 0]
[0, 0, 1]
旋轉矩陣
凸包位置搜尋:
利用向量叉積來取得外圍的點,下面演算法會詳細說明。
禮物包裝演算法
凸多邊形面積計算:
主要是計算兩點x.y的差,就可以取的三角形的底和高,即可計算面積。
面積推算過程
1.測試一,我們可以如下圖來得知最大面積為sqrt(2)。
第一種算法:
我們乘上對邊就可得到鄰邊。鄰邊 = cos(45 - 角度) * sqrt(2)
會發現陰影面積的長*寬 = 鄰邊 * 1 = A面積。
因此我們可以求反三角函數求出角度求出 角度 = 45度 -acos(鄰邊 / 對邊)。
第二種算法(可跳過):
雖然這算法多此一舉就是了,但當時我忘記用45度扣掉所以用另一個角去算,臨時想到的解決方法但不推薦。
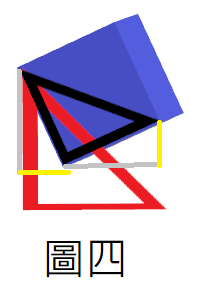
首先圖四灰色線=A,黃色線=B,則我們可以知道A+B=面積,和畢氏定理a^2 + b^2 = sqrt(2)^2,用二元一次方程式解,求得:
a = abs(((-2 * 面積) + sqrt(pow((-2 * 面積), 2) - 8 * (面積 * 面積 - 1))) / 4),算出來的為灰色線,在使用反三角函數得 角度 = asin(A / sqrt(2))
再將角度帶入旋轉公式即可(這部分答案用原始的旋轉公式也可)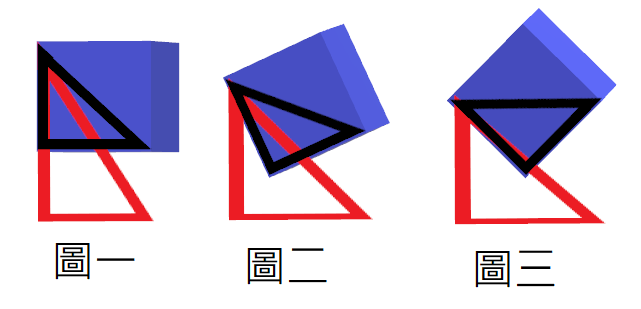
2.測試二,測試二部分我們計算每個角的位置在投影在XZ平面上,使用禮物包裝法點連起來(六邊形),計算面積,使用二分法取得精準度到最少小數點6位。
這部分我延續上面的圖3的位置在往上轉N度會等於最大面積sqrt(3),如圖五,因為最大面積是一個正六邊形,用面積推算回去得到的邊長是1 / sqrt(6)即是圖五黑色底線,這時候得知 角度 = acos(鄰邊 / 斜邊),得到最大角度為35.2644度,因此就可以用二分法從0度到35.2644取的我們的面積來比較。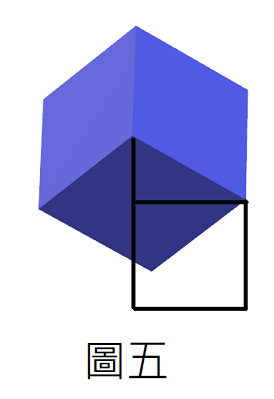
#include <iostream>
#include <vector>
#include "math.h"
#include <algorithm>
using namespace std;
typedef long double LONG_D;
typedef vector<vector<LONG_D>> Matrix;
enum MatrixType
{
DEFAULT,
RotatX,
RotatY,
RotatZ,
};
struct Point
{
Point() : _x(0.0), _y(0.0) {}
Point(const LONG_D x, const LONG_D y) : _x(x), _y(y) {}
LONG_D _x;
LONG_D _y;
};
const LONG_D PI = atan(1) * 4;
//F, G, H, E, B, C, D, A
const Matrix _cubicPoint = { {0.5, 0.5, 0.5},
{ 0.5, 0.5, -0.5 },
{ -0.5, 0.5, -0.5 },
{-0.5, 0.5, 0.5 },
{ 0.5, -0.5, 0.5 },
{ 0.5, -0.5, -0.5 },
{ -0.5, -0.5, -0.5 },
{ -0.5, -0.5, 0.5, } };
inline const LONG_D Ang2Rad(const LONG_D& angle)
{
return angle / 180.0 * PI;
}
inline const LONG_D Rad2Ang(const LONG_D& radian)
{
return radian / PI * 180.0;
}
/* 向量叉積向量。,大於180度叉積 > 0、大於180度叉積 < 0、等於 180° 叉積 = 0
|a|向量 |b| 向量
|a| x |b| = { {|i|, |k|, |j|},
{x1, y1, 0},
{x2, y2, 0} }
解行列式 |j| * (x1 * y2 - x2 * y2) + 0 * (...) + 0 * (....)
推算出來公式: |j| * (x1 * y2 - x2 * y2) 內積大於0度(小於等於則是超過180度,剛好可拿來使用)
*/
inline const bool Cross(const Point& p1, const Point& vertex, const Point& p2)
{
return ((p2._x - vertex._x) * (p1._y - vertex._y) - (p2._y - vertex._y) * (p1._x - vertex._x)) > 0.0;
}
Matrix GetMatrix(const LONG_D& radian, const MatrixType type)
{
Matrix matrix;
switch (type)
{
case RotatX:
matrix = { { 1, 0, 0 },
{ 0, cos(radian), sin(radian) },
{ 0, -sin(radian), cos(radian) } };
break;
case RotatY:
matrix = { { cos(radian), 0, -sin(radian) },
{ 0, 1, 0 },
{ sin(radian), 0, cos(radian) } };
break;
case RotatZ:
matrix = { { cos(radian), sin(radian), 0 },
{ -sin(radian), cos(radian), 0 },
{ 0, 0, 1 } };
break;
case DEFAULT:
matrix = { { 0.5, 0, 0 },
{ 0, 0.5, 0 },
{ 0, 0, 0.5 } };
break;
}
return matrix;
}
Matrix MulMatrix(const Matrix& matrix1, const Matrix& matrix2)
{
Matrix mul(matrix1.size(), vector<LONG_D>(matrix2[0].size(), 0));
for (size_t row = 0; row < matrix1.size(); row++)
{
for (size_t col = 0; col < matrix2[0].size(); col++)
{
for (size_t index = 0; index < matrix2.size(); index++)
{
mul[row][col] += (matrix1[row][index] * matrix2[index][col]);
}
}
}
return mul;
}
vector<LONG_D> MulPoint(const Matrix& matrix1, const vector<LONG_D>& point)
{
vector<LONG_D> mul(matrix1.size(), 0);
for (size_t row = 0; row < matrix1.size(); row++)
{
for (size_t col = 0; col < point.size(); col++)
{
mul[row] += (matrix1[row][col] * point[col]);
}
}
return mul;
}
vector<Point> GetHullPoint(const vector<Point>& rotatePoint)
{
vector<Point> hullPoint;
int start = 0;
for (size_t index = 0; index < rotatePoint.size(); index++)
{
if (rotatePoint[index]._x < rotatePoint[start]._x
|| (rotatePoint[index]._x == rotatePoint[start]._x && rotatePoint[index]._y < rotatePoint[start]._y))
{
start = index;
}
}
int findEnd = start;
while (true)
{
hullPoint.push_back(rotatePoint[findEnd]);
int find = start;
for (size_t index = 0; index < rotatePoint.size(); index++)
{
// 判斷凸型頂點
if (find == findEnd
|| Cross(rotatePoint[index], hullPoint[hullPoint.size() - 1], rotatePoint[find]))
{
find = index;
}
}
findEnd = find;
if (start == find)
{
break;
}
}
return hullPoint;
}
LONG_D GetHullArea(const vector<Point>& point)
{
LONG_D area = 0;
area += abs(point[point.size() - 1]._x * point[0]._y - point[point.size() - 1]._y * point[0]._x);
for (size_t index = 1; index < point.size(); index++)
{
area += abs(point[index - 1]._x * point[index]._y - point[index - 1]._y * point[index]._x);
}
area *= 0.5;
return area;
}
LONG_D GetArea(const Matrix& rotateZ, const LONG_D& radian)
{
const Matrix rotateX = GetMatrix(radian, RotatX);
vector<Point> rotatePoint(_cubicPoint.size());
// 原始座標, 對Z軸心旋轉45度, 對X軸心旋轉radian弧度, 投影在X.Z, 取得2D座標
for (size_t index = 0; index < _cubicPoint.size(); index++)
{
vector<LONG_D> point = MulPoint(rotateX, rotateZ[index]);
rotatePoint[index] = Point(point[0], point[2]);
}
vector<Point> hullPoint = GetHullPoint(rotatePoint);
LONG_D area = GetHullArea(hullPoint);
return area;
}
Matrix Compute(const LONG_D& area)
{
if (area <= sqrt(2))
{
//const LONG_D aLen = abs(((-2 * area) + sqrt(pow((-2 * area), 2) - 8 * (area * area - 1))) / 4); // a^2.....
//const LONG_D radian = asin(aLen);
LONG_D radian = Ang2Rad(45.0) - abs(acos(area / sqrt(2)));
const Matrix rotateZ = GetMatrix(radian, RotatZ);
return MulMatrix(rotateZ, GetMatrix(0, DEFAULT));
}
const Matrix rotateZ = GetMatrix(Ang2Rad(45.0), RotatZ);
Matrix rotateZPoint(8);
for (size_t index = 0; index < _cubicPoint.size(); index++)
{
rotateZPoint[index] = MulPoint(rotateZ, _cubicPoint[index]);
}
LONG_D minRadian = Ang2Rad(0);
LONG_D maxRadian = Ang2Rad(35.2644);
LONG_D nowRadian = maxRadian;
LONG_D nowArea = GetArea(rotateZPoint, maxRadian);
while (abs(area - nowArea) > 0.00000000001)
{
const LONG_D middleRadian = (minRadian + maxRadian) / 2.0;
const LONG_D middleArea = GetArea(rotateZPoint, middleRadian);
if (area >= middleArea)
{
minRadian = middleRadian;
}
else
{
maxRadian = middleRadian;
}
nowRadian = middleRadian;
nowArea = middleArea;
}
Matrix rotateX = GetMatrix(nowRadian, RotatX);
Matrix matrix (3);
for (int index = 0; index < 3; index++)
{
vector<LONG_D> center(3, 0);
center[index] = 0.5;
matrix[index] = MulPoint(rotateX, MulPoint(rotateZ, center));
}
return matrix;
}
void Print(Matrix& matrix, const int index)
{
cout.precision(16);
cout << "Case #" << index + 1 << ":" << endl;
for (size_t row = 0; row < matrix.size(); row++)
{
for (size_t col = 0; col < matrix.size(); col++)
{
cout << matrix[row][col] << " ";
}
cout << endl;
}
}
void Input()
{
int testCount = 0;
while (cin >> testCount)
{
LONG_D area = 0L;
for (int index = 0; index < testCount; index++)
{
cin >> area;
Matrix result = Compute(area);
Print(result, index);
}
}
}
int main()
{
Input();
return 0;
}
1.宣告兩個別名LONG_D和Matrix,方便觀看。
2.宣告旋轉類型MatrixType。
3.建立一個結構Point用來記錄2D座標。
4.計算PI的弧度(因C++都是用弧度運算)。
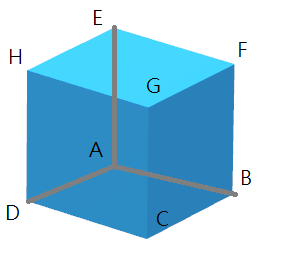
5.宣告和指派8個頂點位置給_cubicPoint如下圖
註:題目說八個角為+-0.5km。
6.Ang2Rad角度轉弧度。
7.Rad2Ang弧度轉角度。
8.GetMatrix部分為得取旋轉矩陣或原始x.y.z座標矩陣。
註:原始為何是0.5? 題目說原點是(0,0,0)是頂點中心,也就是頂點到頂點 / 2 = 原始座標。
我放大到200如下方程式碼的x.y.z的座標,並畫出它在2D中的顯示,如下圖。
3D轉2D公式:
X = 原點X - cos(45度) * x(X水平投影) + y大小
Y = 原點Y + sin(45度) * x(X在垂直向上的投影) - z大小
因為Z和X如果垂直那Y就會往45度方向所以才會這樣計算,可以自己推算看看。
----------C#--3D轉2D可視化START---------
//x = origin - cos(45) * x + y; //原點X - cos(45度) * x(X水平投影) + y大小
//y = origin + sin(45) * x - z; //原點Y + sin(45度) * x(X在垂直向上的投影) - z大小
public Point2D GetPoint2D(Point3D origin)
{
int x = (int)(origin.X - Math.Cos(45) * _x + _y);
int y = (int)(origin.Y + Math.Sin(45) * _x - _z);
return new Point2D(x, y);
}
Point3D origin = new Point3D(300, 300, 300);
Point3D xEnd = new Point3D(200, 0, 0);
Point3D yEnd = new Point3D(0, 200, 0);
Point3D zEnd = new Point3D(0, 0, 200);
Point2D xLine = xEnd.GetPoint2D(origin);
e.Graphics.DrawLine(pen, origin.X, origin.Y, xLine.X, xLine.Y);
Point2D yLine = yEnd.GetPoint2D(origin);
e.Graphics.DrawLine(pen, origin.X, origin.Y, yLine.X, yLine.Y);
Point2D zLine = zEnd.GetPoint2D(origin);
e.Graphics.DrawLine(pen, origin.X, origin.Y, zLine.X, zLine.Y);
----------C#--3D轉2D可視化END---------
9.MulMatrix為矩陣相乘,左矩陣的水平列每一個對上右矩陣垂直行兩兩相乘再加總。
如下範例:
[1, 2, 3] [1, 3, 4]
A = [4, 5, 6] X [2, 2, 2]
[4, 5, 6] [3, 1, 5]
A[0][0] = (1 * 1) + (2 * 2) + (3 * 3)
A[0][1] = (1 * 3) + (2 * 2) + (3 * 1)
A[0][2] = (1 * 4) + (2 * 2) + (3 * 5)
A[1][0] = (4 * 1) + (5 * 2) + (6 * 3)
.....略。
10.MulPoint是計算頂點在矩陣旋轉後的座標如上一樣,只是右矩陣只有一列水平列。
typedef long double LONG_D;
typedef vector<vector<LONG_D>> Matrix;
enum MatrixType
{
DEFAULT,
RotatX,
RotatY,
RotatZ,
};
struct Point
{
Point() : _x(0.0), _y(0.0) {}
Point(const LONG_D x, const LONG_D y) : _x(x), _y(y) {}
LONG_D _x;
LONG_D _y;
};
const LONG_D PI = atan(1) * 4;
//F, G, H, E, B, C, D, A正方體頂點位置
const Matrix _cubicPoint = { {0.5, 0.5, 0.5},
{ 0.5, 0.5, -0.5 },
{ -0.5, 0.5, -0.5 },
{-0.5, 0.5, 0.5 },
{ 0.5, -0.5, 0.5 },
{ 0.5, -0.5, -0.5 },
{ -0.5, -0.5, -0.5 },
{ -0.5, -0.5, 0.5, } };
// 角度轉弧度
inline const LONG_D Ang2Rad(const LONG_D& angle)
{
return angle / 180.0 * PI;
}
// 弧度轉角度
inline const LONG_D Rad2Ang(const LONG_D& radian)
{
return radian / PI * 180.0;
}
// 得取旋轉矩陣或原點位置
Matrix GetMatrix(const LONG_D& radian, const MatrixType type)
{
Matrix matrix;
switch (type)
{
case RotatX:
matrix = { { 1, 0, 0 },
{ 0, cos(radian), sin(radian) },
{ 0, -sin(radian), cos(radian) } };
break;
case RotatY:
matrix = { { cos(radian), 0, -sin(radian) },
{ 0, 1, 0 },
{ sin(radian), 0, cos(radian) } };
break;
case RotatZ:
matrix = { { cos(radian), sin(radian), 0 },
{ -sin(radian), cos(radian), 0 },
{ 0, 0, 1 } };
break;
case DEFAULT:
matrix = { { 0.5, 0, 0 },
{ 0, 0.5, 0 },
{ 0, 0, 0.5 } };
break;
}
return matrix;
}
// 矩陣相乘
Matrix MulMatrix(const Matrix& matrix1, const Matrix& matrix2)
{
Matrix mul(matrix1.size(), vector<LONG_D>(matrix2[0].size(), 0));
for (size_t row = 0; row < matrix1.size(); row++)
{
for (size_t col = 0; col < matrix2[0].size(); col++)
{
for (size_t index = 0; index < matrix2.size(); index++)
{
mul[row][col] += (matrix1[row][index] * matrix2[index][col]);
}
}
}
return mul;
}
// 頂點乘上旋轉矩陣
vector<LONG_D> MulPoint(const Matrix& matrix1, const vector<LONG_D>& point)
{
vector<LONG_D> mul(matrix1.size(), 0);
for (size_t row = 0; row < matrix1.size(); row++)
{
for (size_t col = 0; col < point.size(); col++)
{
mul[row] += (matrix1[row][col] * point[col]);
}
}
return mul;
}
1.testCount測試資料T筆數。
2.area為面積大小。
3.Compute函數開始計算旋轉矩陣。
4.Print輸出回傳結果。
void Input()
{
int testCount = 0;
while (cin >> testCount)
{
LONG_D area = 0;
for (int index = 0; index < testCount; index++)
{
cin >> area;
Matrix result = Compute(area);
Print(result, index);
}
}
}
1.如果面積小於等於sqrt(2)(測資一)可以用我們分析的公式直接解決。
2.先把45度轉弧度再帶入公式得到角度。
3.我們選擇繞著Z軸轉,得取Z軸的樣板rotateZ。
4.MulMatrix將Z軸樣板乘上原始的座標即是我們所要的答案(這部分其實應該座標對旋轉矩陣乘)。
Matrix Compute(const LONG_D& area)
{
if (area <= sqrt(2))
{
//const LONG_D aLen = abs(((-2 * area) + sqrt(pow((-2 * area), 2) - 8 * (area * area - 1))) / 4); // a^2.....
//const LONG_D radian = asin(aLen);
LONG_D radian = Ang2Rad(45.0) - abs(acos(area / sqrt(2)));
const Matrix rotateZ = GetMatrix(radian, RotatZ);
return MulMatrix(rotateZ, GetMatrix(0, DEFAULT));
}
}
若大於sqrt(2)我們就要旋轉兩次,這部分可以優化(官方的分析有影片)。
1.首先我先直接取得我們剛剛的旋轉Z軸模板=第一次旋轉。
2.Z軸模板乘上rotateZPoint 8個頂點,得取目前8個頂點的三維座標。
3.設定目前最大最小的弧度與目前弧度(minRadian.maxRadian.nowRadian)和面積(nowArea)。
4.使用二分搜尋,取得兩弧度中間,GetArea計算面積(若要理解下方還有說明函數)。
若A面積>中間面積則範圍縮小為中間值~最大面積,反之,A面積<中間面積則範圍縮小為最小面積~中間值,再將目前面積設定為中間面積,直到精準度到達6位。
5.使用我們計算好的弧度得取旋轉X軸的模板,這裡使用迴圈跑三次將x.y.z原本的三個點先乘上Z再乘上X(不得交換先旋轉哪一個就必須先乘上哪個矩陣)。
Matrix Compute(const LONG_D& area)
{
const Matrix rotateZ = GetMatrix(Ang2Rad(45.0), RotatZ);
Matrix rotateZPoint(8);
for (size_t index = 0; index < _cubicPoint.size(); index++)
{
rotateZPoint[index] = MulPoint(rotateZ, _cubicPoint[index]);
}
LONG_D minRadian = Ang2Rad(0);
LONG_D maxRadian = Ang2Rad(35.2644);
LONG_D nowRadian = maxRadian;
LONG_D nowArea = GetArea(rotateZPoint, maxRadian);
while (abs(area - nowArea) > 0.00000000001)
{
const LONG_D middleRadian = (minRadian + maxRadian) / 2.0;
const LONG_D middleArea = GetArea(rotateZPoint, middleRadian);
if (area >= middleArea)
{
minRadian = middleRadian;
}
else
{
maxRadian = middleRadian;
}
nowRadian = middleRadian;
nowArea = middleArea;
}
Matrix rotateX = GetMatrix(nowRadian, RotatX);
Matrix matrix (3);
for (int index = 0; index < 3; index++)
{
vector<LONG_D> center(3, 0);
center[index] = 0.5;
matrix[index] = MulPoint(rotateX, MulPoint(rotateZ, center));
}
return matrix;
}
1.我們用傳入的已旋轉45度Z的八個頂點座標乘上目前我們預測radian的X旋轉樣板,因為我們投影在XZ平面所以我們只需要取的X和Z的做邊轉換到2D平面。
2.GetHullPoint取得投影在2D的凸多邊型頂點座標(若要理解下方還有說明函數)。
3.GetHullArea取得凸多邊形面積(若要理解下方還有說明函數)。
LONG_D GetArea(const Matrix& rotateZ, const LONG_D& radian)
{
const Matrix rotateX = GetMatrix(radian, RotatX);
vector<Point> rotatePoint(_cubicPoint.size());
// 原始座標, 對Z軸心旋轉45度, 對X軸心旋轉radian弧度, 投影在X.Z, 取得2D座標
for (size_t index = 0; index < _cubicPoint.size(); index++)
{
vector<LONG_D> point = MulPoint(rotateX, rotateZ[index]);
rotatePoint[index] = Point(point[0], point[2]);
}
vector<Point> hullPoint = GetHullPoint(rotatePoint);
LONG_D area = GetHullArea(hullPoint);
return area;
}
1.GetHullPoint參照一個容器2D座標過去即可計算。
2.先宣告一個容器紀錄頂點,和宣告並指派start用來記錄第一個最左邊的。
3.跑回圈搜尋目前最左邊的點,就是搜尋最小x和y座標,並在指派給start。
4.在宣告一個findEnd來記錄每次尋找凸點最左邊的索引位置,先暫時指派最左邊的索引值。
5.開始跑回圈直到我們跑回第一個最左邊的點。
6.先把上一個我們找到的findEnd點加入,在宣告一個我們目前找到左邊的索引位置find,暫時指派第一個最左邊位置 給他。
7.跑回圈尋找最左邊的點。
8.先判斷find == findEnd因為上一個已經是頂點所以將當下索引設定為我們目前找到的在繼續比較。
例如上一輪找到5當索引值到5時我們比較叉積時候他又在左邊find就變成5,然而5已經在上一輪被設定過,我們必須跳過他先將6設定為我們找到的。
9.在判斷叉積Cross傳入兩個2D座標和一個vertex頂點(上一個凸點)方可計算叉積(註解有打公式),下方我用我的方式解釋。
假如vertex(1,2)是我們找到的上一個最左邊的點。
* * * * * *
* * x * * *
* * * x * *
* 1 * * * *
* * * * * *
* * * * * *
公式 ((p2._x - vertex._x) * (p1._y - vertex._y)
- (p2._y - vertex._y) * (p1._x - vertex._x))
1.vertex = (1,2)
p1 = (3,3)
p2 = (2,4)
(2 - 1) * (3 - 2) - (4 - 2) * (3 - 2) = -1
2.vertex = (1,2)
p1 = (2,4)
p2 = (3,3)
(3 - 1) * (4 -2) - (3 - 2) * (2 - 2) = 2 * 2 = 4
第一假如(3,3)是我們現在找到的點,(2,4)是上個被找到的點,算出結果為負數。
第二假如(2,4)是我們現在找到的點,(3,3)是上個被找到的點,算出結果為正數。
這是運用叉積運算來計算出向量的差,因為180度的向量不會是負的。
若還需要更詳細正確的原理可上網搜尋。
10.若已經搜尋完我們將findEnd指派find給他,若find等於我們第一個最左邊的代表凸點都已經搜尋到,即可結束。
vector<Point> GetHullPoint(const vector<Point>& rotatePoint)
{
vector<Point> hullPoint;
int start = 0;
for (size_t index = 0; index < rotatePoint.size(); index++)
{
if (rotatePoint[index]._x < rotatePoint[start]._x
|| (rotatePoint[index]._x == rotatePoint[start]._x
&& rotatePoint[index]._y < rotatePoint[start]._y))
{
start = index;
}
}
int findEnd = start;
while (true)
{
hullPoint.push_back(rotatePoint[findEnd]);
int find = start;
for (size_t index = 0; index < rotatePoint.size(); index++)
{
// 判斷凸型頂點
if (find == findEnd
|| Cross(rotatePoint[index], hullPoint[hullPoint.size() - 1], rotatePoint[find]))
{
find = index;
}
}
findEnd = find;
if (start == find)
{
break;
}
}
return hullPoint;
}
/* 向量叉積向量。,大於180度叉積 > 0、大於180度叉積 < 0、等於 180° 叉積 = 0
|a|向量 |b| 向量
|a| x |b| = { {|i|, |k|, |j|},
{x1, y1, 0},
{x2, y2, 0} }
解行列式 |j| * (x1 * y2 - x2 * y2) + 0 * (...) + 0 * (....)
推算出來公式: |j| * (x1 * y2 - x2 * y2) 內積大於0度(小於等於則是超過180度,剛好可拿來使用)
*/
inline const bool Cross(const Point& p1, const Point& vertex, const Point& p2)
{
return ((p2._x - vertex._x) * (p1._y - vertex._y) - (p2._y - vertex._y) * (p1._x - vertex._x)) > 0.0;
}
1.GetHullArea傳入凸點座標。
2.我們去計算點到點的x.y在算出三角形面積,上面有推倒文章公式。
例如,我們有A座標B座標C座標D座標。
開始計算A->B兩點的x和y所組成的三角形,在計算B->C兩點,在計算C->D兩點,最後在計算D->A兩點。
你可以想像它計算方式就是切割出很多個長方形在計算三角形面積。
若想更瞭解可以詳看過程,就可得知為何要這樣做。
面積推算過程
LONG_D GetHullArea(const vector<Point>& point)
{
LONG_D area = 0;
area += abs(point[point.size() - 1]._x * point[0]._y - point[point.size() - 1]._y * point[0]._x);
for (size_t index = 1; index < point.size(); index++)
{
area += abs(point[index - 1]._x * point[index]._y - point[index - 1]._y * point[index]._x);
}
area *= 0.5;
return area;
}
這題目最快解法大概是計算向量或是運用正方體最高點的距離差去計算,但這些都牽扯到滿多數學,對我平常很少在用幾何的人可能要花更多時間去了解,但最開心的是多學到一種演算法(禮物包裝演算法)。
這篇文章實在有夠長,仔細看其實每個部份就是一小塊演算法組合起來,打那麼長
有筆誤或理解錯的希望大家包涵。
